在R內實踐百分位數回歸 (Doing Quantile Regression in R statistical software)

    近日不約而同地有3位碩士研究生, 都問了類似的問題: “老師, 我想做回歸分析, 而應變項雖然是連續性變項, 但郤是偏態的, 怎麼辦好?”

    於是我都要她們複習一下線性回歸的基本要求, 握要地說是”LINE”, 要求變項:

1. “L”: 是線性的 (連續性數據)
2. “I”: 變項間是互相獨立 (不要有多重共線性)
3. “N”: 要正態分佈
4. “E”: 誤差獨立分佈

    現實中”L”和”E” 基本都是滿足的, 但”I”和”N”就未必了… 人們是睿智的, 想到解決”I”和”N”的問題是:

1. “I”---岭回歸, 主成分分析, 或只選擇最相關的變項作回歸分析;
2. “N”---百分位數回歸…

現在主要介紹百分位數回歸! 其本質是求解任何分位值時, 各引數 x 的回歸係數。其能在一定程度上全面展示所有資料的資訊，但更側重於對特徵分佈不同位置人群的異質性分析。它不僅可以度量回歸變數在分佈中心的影響，而且還可以度量在分佈上尾和下尾的影響，因此較之傳統線性回歸模型具有獨特的優勢，能夠得到全面的分析結果，尤其適用於不均勻的條件分佈，且分位數回歸係數較傳統線性回歸模型的係數估計更穩健。

進行百分位數回歸的統計軟件主要有SAS, R, STATA等, 但以SAS及R為普遍! 在SAS內以proc quantreg為操作步驟. 在R內則以quantreg統計包為主. 現以R為介紹, 並使用quantreg統計包內自帶的數據engel示範…

library(quantreg)  #安裝及使用quantreg統計包 : install.packages(“quantreg”)

data("engel")  #使用自帶的數據engel

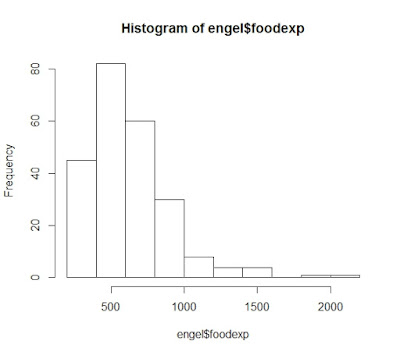
food.nor<-shapiro.test(engel$foodexp)  #數據庫內foodexp的正態性檢驗

food.hist<-hist(engel$foodexp)  #作個直條圖

   Shapiro-Wilk normality test

data:  engel$foodexp

W = 0.87471, p-value = 5.45e-13

(明顯地是偏態分佈啦...)

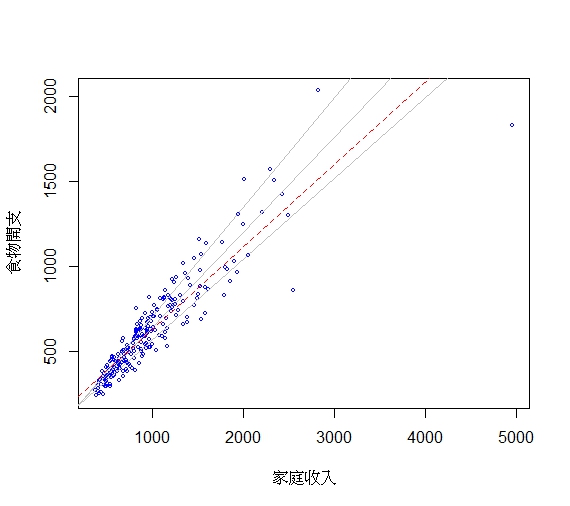
fit=rq(foodexp~income,data=engel,tau=c(0.25,0.5,0.75))  #百分位數回歸: 命令rq, 公式foodexp~income, 使用數據庫engel, 百分位數0.25下四分位數,0.5中位數,0.75上四分位數

summary(fit)  #算出總結果

plot(summary(fit))  #對結果作圖

 

attach(engel)  #打開engel資料集，直接運行其中的列名，就可以調用相應列

plot(income,foodexp,cex=0.25,type="n", xlab="家庭收入", ylab="食物開支")  # 畫圖

points(income,foodexp,cex=0.5,col="blue")  # 添加點，點的大小為0.5

abline( rq(foodexp ~ income, tau=0.5), col="blue" )  # 畫中位數回歸的擬合直線，顏色藍

abline( lm(foodexp ~ income), lty = 2, col="red" )  # 畫普通最小二乘法擬合直線，顏色紅

taus<-c(0.25, 0.5, 0.75)

for(i in 1:length(taus)){  # 繪製不同分位點下的擬合直線，顏色為灰色

  abline( rq(foodexp ~ income, tau=taus[i]), col="gray" )

}

detach(engel)

 參考資料:

研究健康相关生命质量影响因素的分位数回归分析. 中国卫生统计2016年4月第33卷第2期.P190-193.

分位数回归及应用简介. 统计与信息论坛. 第21卷第3期2006年5月.P35-38.